Have you ever wanted to query an online application but felt sceptical about sharing your personal data? How can confidential data be given to a third party for analysis without worrying about its privacy implications? How do multiple competing organisations collaborate on a joint task without revealing their private data? Private data is not limited to personally identifiable information and healthcare records, it is much more than that. It is any data that one does not wish to reveal to others, such as personal preferences, online activities, and purchase history. The goal is to leverage such private data from multiple parties to conduct joint operations while safeguarding data privacy.

A commonly employed solution involves a trusted third party that collects private data from all parties, performs the computation, and returns the result to each party [1]. While this approach is fast, it has a drawback – the trusted party possesses the private data of all parties and full control over the output, making it a single point of vulnerability. Therefore, it is essential to assume that all parties in the transaction do not trust each other; in other words, they are mutually distrusting. There are two primary approaches to conducting computations on private data from mutually distrusting parties: Homomorphic Encryption and Secure Multi-Party Computation.

Homomorphic Encryption

In Homomorphic Encryption, each party encrypts its private data. The computations are performed directly on the encrypted data by a third party, and the obtained output is also in encrypted form. Each party sends the encrypted data to a third party, who performs the computation without decrypting the private data [8]. However, it’s important to note that homomorphic encryption is computationally intensive and time-consuming, taking anywhere from a few seconds to several days to complete the computation.

Secure Multi-Party Computation

Alternative approaches employ Secure Multi-Party Computation (SMPC) protocols to provide similar security guarantees as Homomorphic Encryption but with a significant reduction in computation time. SMPC protocols are cryptographic protocols designed to execute operations on private data from various sources/parties, ensuring that no party possesses sufficient information to reconstruct the private data of other parties.

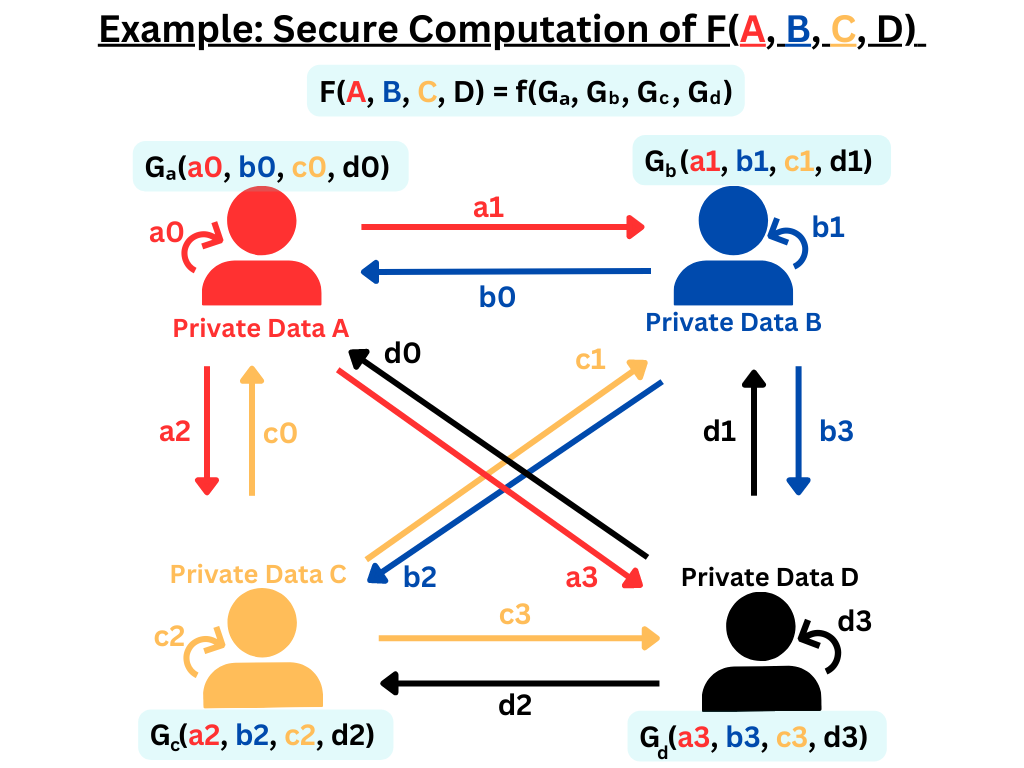
Mutually distrusting parties jointly perform the required computation by communicating with each other without disclosing their private data and without inferring the private data of other parties.

Consider the scenario illustrated in Figure 1. Four parties are involved in this scenario, each possessing data required for securely computing a function, F. Let’s designate these parties as party 0 (holding data A), party 1 (holding data B), party 2 (holding data C), and party 3 (holding data D). In this example, each party generates random shares of its private data. For instance, party 0 splits its private data A into random shares a0, a1, a2, and a3. These shares are then distributed to party 0, party 1, party 2, and party 3 respectively. Each party upon receiving the random shares of all the parties, computes it’s local function, G, on the received shares. The local computations collectively yield results that, when combined with those of other parties, enable the reconstruction of the final answer for the function F(A, B, C, D). Importantly, none of the parties can gain knowledge of the private data held by the others solely by using the received random shares. The protocol is designed to ensure that the local function G and the subsequent reconstruction consistently provide the correct answer for F, all while preserving the confidentiality of the private data.

The function F can be computed using various Secure Multi-Party Computation (SMPC) protocols, like Yao’s garbled circuits [2], Shamir secret sharing [3], and the ABY2.0 protocol [4]. Further, each SMPC protocol is designed to meet the essential conditions of privacy and correctness.

1. Privacy: It ensures that the parties only gain knowledge that can be inferred from the output. They gain no additional information on the private data of other parties.
2. Correctness: It guarantees that the parties receive the correct output.

Note that, in contrast to homomorphic encryption, SMPC distributes computation among the involved parties, allowing operations to be performed on unencrypted data. Further, as SMPC operates directly on unencrypted data, resulting in a faster computation compared to homomorphic encryption. However, this efficiency comes with a trade-off of additional rounds of communication, representing a minimal computational overhead.

Applications of SMPC

The first significant real-world implementation of Secure Multi-Party Computation (SMPC) occurred in the auctioning of sugar beet contracts to Danish farmers, all while preserving the confidentiality of bids [5]. In this application, only the ultimate winning bid was disclosed to all participants. The crucial requirements were to prevent any player from learning about the bids of others (ensuring privacy) and to ensure bid independence, meaning no player could strategically place a related bid to secure the contract. As a successful outcome, approximately 25,000 tons of sugar beet production rights were securely transferred using SMPC.

SMPC protocols were implemented in Boston to analyse wage disparities based on gender and ethnicity within organisations [6]. The Boston Women’s Workforce Council aimed to address wage gaps for women and ethnic groups by collecting, analysing, and reporting payroll data from over 100 organisations in Boston. Given the sensitive nature of payroll datasets, ensuring the confidentiality of each organisation’s data was a significant concern. Researchers from Boston University successfully used SMPC to securely analyse wage data, effectively mitigating privacy concerns in this collaborative effort for wage equality.

SMPC demonstrates its versatility by enabling the comparison and analysis of an individual’s private DNA data against a database of cancer patients’ DNA for cancer diagnosis [7]. Its applications extend to secure voting, collaborative financial fraud detection, collaborative health monitoring, and more. This represents just the beginning of what SMPC can contribute to global data privacy and policy making. After decades of theoretical research and practical solutions, SMPC has proven its robustness. It stands poised to play a crucial role in safeguarding personal data privacy and promoting secure data utilisation.

Author:
Rashmi T
Dr Haritha Kallamadi

References

1. Evans, D., Kolesnikov, V., & Rosulek, M. (2018). A pragmatic introduction to secure multi-party computation. Foundations and Trends® in Privacy and Security, 2(2-3), 70-246.
2. Yao, A. C. C. (1986, October). How to generate and exchange secrets. In 27th annual symposium on foundations of computer science (Sfcs 1986) (pp. 162-167). IEEE.
3. Shamir, A. (1979). How to share a secret. Communications of the ACM, 22(11), 612-613.
4. Patra,A., Schneider, T., Suresh, A., & Yalame, H. (2021, August). ABY2. 0: Improved Mixed-Protocol Secure Two-Party Computation. In USENIX Security Symposium (pp. 2165-2182).
5. Bogetoft, P., Christensen, D. L., Damgård, I., Geisler, M., Jakobsen, T., Krøigaard, M., … & Toft, T. (2009). Secure multiparty computation goes live. In Financial Cryptography and Data Security: 13th International Conference, FC 2009, Accra Beach, Barbados, February 23-26, 2009. Revised Selected Papers 13 (pp. 325-343). Springer Berlin Heidelberg.
6. Bestavros, A., Lapets, A., & Varia, M. (2017). User-centric distributed solutions for privacy-preserving analytics. Communications of the ACM, 60(2), 37-39.
7. Lindell, Y. (2020). Secure multiparty computation. Communications of the ACM, 64(1), 86-96.
8. Abbas Acar, Hidayet Aksu, A. Selcuk Uluagac, and Mauro Conti. 2018. A Survey on Homomorphic Encryption Schemes: Theory and Implementation. ACM Comput. Surv. 51, 4, Article 79 (July 2019), 35 pages. https://doi.org/10.1145/3214303